内排序(八):基数排序
2012-08-04 23:54:10分配排序的基本思想:排序过程无须比较关键字,而是通过“分配”和“收集”过程来实现排序。它们的时间复杂度可达到线性阶:O(n)。
一、两种多关键码排序方法
最高位优先法(MSD法)。先按k1排序,将序列分成若干子序列,每个子序列中的记录具有相同的k1值;再按k2排序,将每个子序列分成更小的子序列;然后,对后面的关键码继续同样的排序分成更小的子序列,直到按kd排序分组分成最小的子序列后,最后将各个子序列连接起来,便可得到一个有序的序列。前面介绍的扑克牌先按花色再按面值进行排序的方法就是MSD法 最次位优先法(LSD法)。先按kd排序,将序列分成若干子序列,每个子序列中的记录具有相同的kd值;再按kd-1排序,将每个子序列分成更小的子序列;然后,对后面的关键码继续同样的排序分成更小的子序列,直到按k1排序分组分成最小的子序列后,最后将各个子序列连接起来,便可得到一个有序的序列。前面介绍的扑克牌先按面值再按花色进行排序的方法就是LSD法。
二、基于LSD方法的链式基数排序的基本思想
“多关键字排序”的思想实现“单关键字排序”。对数字型或字符型的单关键字,可以看作由多个数位或多个字符构成的多关键字,此时可以采用“分配-收集”的方法进行排序,这一过程称作基数排序法,其中每个数字或字符可能的取值个数称为基数。比如,扑克牌的花色基数为4,面值基数为13。在整理扑克牌时,既可以先按花色整理,也可以先按面值整理。按花色整理时,先按红、黑、方、花的顺序分成4摞(分配),再按此顺序再叠放在一起(收集),然后按面值的顺序分成13摞(分配),再按此顺序叠放在一起(收集),如此进行二次分配和收集即可将扑克牌排列有序。
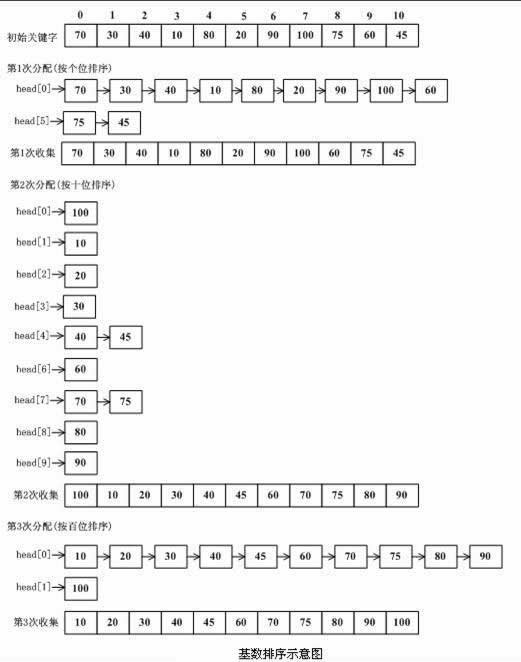
三、基数排序的实现
public class RadixNode<T>
{
private T data; //数据域
private RadixNode<T> next; //引用域
public RadixNode(T val, RadixNode<T> p)
{
data = val;
next = p;
}
public RadixNode(RadixNode<T> p)
{
next = p;
}
public RadixNode(T val)
{
data = val;
next = null;
}
public RadixNode()
{
data = default(T);
next = null;
}
//数据域属性
public T Data
{
get
{
return data;
}
set
{
data = value;
}
}
//引用域属性
public RadixNode<T> Next
{
get
{
return next;
}
set
{
next = value;
}
}
}
public class RadixSort
{
public static List<int> Demo(List<int> data)
{
var maxDigit = data.Count;
var mod = 10;
var dev = 1;
for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10)
{
Dictionary<int, List<int>> _counter = new Dictionary<int, List<int>>();
for (var j = 0; j < data.Count; j++)
{
var bucket = ((data[j] % mod) / dev);
if (!_counter.ContainsKey(bucket))
{
_counter[bucket] = new List<int>();
}
_counter[bucket].Add(data[j]);
}
var pos = 0;
for (var j = 0; j <= _counter.Count; j++)
{
if (_counter.ContainsKey(j))
{
while (_counter[j].Count != 0)
{
data[pos++] = _counter[j][0];
_counter[j].RemoveAt(0);
}
}
}
}
return data;
}
}
四、时间复杂度分析
时间效率:设待排序列为n个记录,d个关键码,关键码的取值范围为radix,则进行链式基数排序的时间复杂度为O(d(n+radix)),其中,一趟分配时间复杂度为O(n),一趟收集时间复杂度为O(radix),共进行d趟分配和收集。

